Intransitivity #
Summary #
In math, transitivity is a property of relations such that if A is related to B, and B is related to C, then A is related to C in the same way.
An intransitive relation is one in which this pattern does not hold.
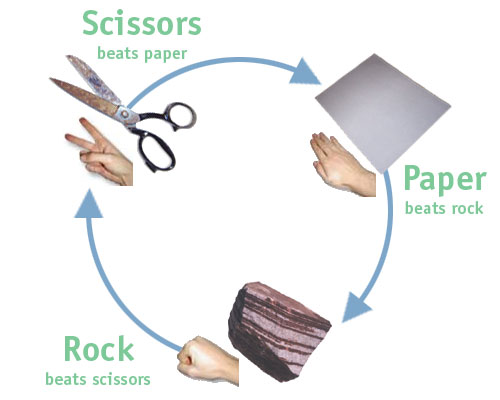
I have a hard time believing that paper beats rock.
(Image: Wikimedia)
Commentary #
I've often thought that there is a bias towards thinking that most relations are transitive. But transitivity is actually a rare case. It makes reasoning simpler (e.g., the friend of my friend is my friend), but is often simply not true: If Bob is friends with Alice and Alice is friends with Eve, Bob might not actually be friends with Eve.
Most preferences are intransitive which is why we have a hard time choosing among multiple options and why voting paradoxes exist. Moreover, most real options involve multiple dimensions, so we run the risk of errors of multiple comparisons.
So, you're trying to pick a movie to watch? (Let's leave out other people's preferences for this example.) Say you prefer movie X over Y and Y over Z. However, when you compare X and and Z, you find that you like Z better. Yep, you're either comparing different features between the films, or the "prefer movie X to movie Y" relation is intransitive.
Keep this in mind next time you catch yourself or others assuming that a relation is transitive.
See Also #
- Intransitivity at Wikipedia for a more rigorous definition.